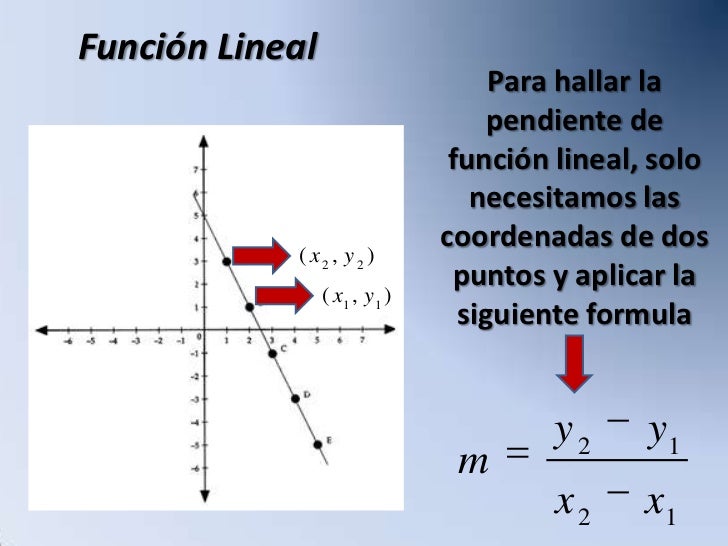
Probabilidad

PROBABILIDADAD

Las probabilidades constituyen una rama de las matemáticas que se ocupa de medir o determinar cuantitativamente la posibilidad de que un suceso o experimento produzca un determinado resultado. La probabilidad está basada en el estudio de la combinatoria y es fundamento necesario de la estadística.

La probabilidad matemática comenzó como un intento de responder a varias preguntas que surgían en los juegos de azar, por ejemplo saber cuántas veces se han de lanzar un par de dados para que la probabilidad de que salga seis sea el 50 por ciento.

Problemas

Una persona puso una contraseña en un archivo de su computadora y sólo recuerda que eran cuatro digitos diferentes. ¿Cúal es la probabilidad de que acierte en el primer intento?

10.9.8.7= 5040               1                                                                                                                                              5040  1 de 5040 de probabilidad.

Se tira un dado equilibrado cinco veces. ¿ Cual es la probabilidad de sacar 6 en todos los tiros?

2 dados----- 1  ( casos favorables)

                      36= 6^2 ( casos posibles)

3 dados------ 1 

                    6^3

5 dados----- 1 

                    6^5=7776

Trigonometría

Trigonometría

CUADRANTES

Por ejemplo: un angulo de 220° se ubicaría en el cuadrante 3.

                     un angulo de 70° en el cuadrante 1.

                     un angulo de 110° en el cuadrante 2.

Ángulos complementarios: son aquellos cuya suma es 90°

Ejemplo: el complemento de un angulo de 60° es 30°.

Ángulos suplementarios: son aquellos cuya suma es 180°

Ejemplo: el suplemento de un angulo de 60° es 120°

Problemas:
1) Un ángulo de un triangulo rectángulo mide 47° y el cateto opuesto 8 cm, hallar la hipotenusa.
Se calcula el  seno    =  cat puesto
                                           hipotenusa

                       sen 47 =  8 cm
                                       hip 
                        hip      =  8 cm 
                                       sen 47 
               
                        hip      =10,9 cm

2)

Se resuelve utilizando la formula de la tangente:

Tg         =        cat puesto
                      cat adyacente 

Tg 30°   =      cat puesto
                           10 cm

Tg 30° x 10 cm = cat opuesto

cat puesto   =   5 cm

Función lineal

FUNCIÓN LINEAL:

Para que una recta sea paralela debe tener las pendientes iguales.

Para que una recta sea perpendicular debe tener las pendientes opuestas e inversas.

f(x)= A.x + b

A es la pendiente. Si A es mayor a 0, la función es creciente.

                              Si A es menor a 0, la función es decreciente.

                              Si A es igual a 0. la función es constante.

B es la ordenada al origen

Función cuadrática

FUNCIÓN CUADRÁTICA

Una función cuadrática es aquella que puede escribirse como una ecuación de la forma:

f(x) = a.x 2 + b.x + c

donde a , b y c (llamados términos ) son números reales cualquieras y a es distinto de cero (puede ser mayor o menor que cero, pero no igual que cero). El valor de b y de c sí puede ser cero .

En la ecuación cuadrática cada uno de sus términos tiene un nombre.

a.x 2 es el término cuadrático

b.x es el término lineal

c es el término independiente

Si pudiésemos representar en una gráfica "todos" los puntos de una función cuadrática , obtendríamos siempre una curva llamada parábola .

Decimos que una parábola es la representación gráfica de una función cuadrática 

Dicha parábola tendrá algunas características o elementos  dependiendo de los valores de la ecuación que la generan.

Estas características o elementos son:

Orientación o concavidad (ramas o brazos)

Puntos de corte con el eje de abscisas (raíces)

Punto de corte con el eje de ordenadas

Eje de simetría

Vértice.

Orientación o concavidad

Una primera característica es la orientación o concavidad de la parábola. Hablamos de parábola cóncava si sus ramas o brazos se orientan hacia arriba y hablamos de parábola convexa si sus ramas o brazos se orientan hacia abajo.

Esta distinta orientación está definida por el valor (el signo) que tenga el término cuadrático (la ax 2 ) :

Si  a > 0 (positivo) la parábola es cóncava o con puntas hacia arriba, como en f(x) = 2x 2 − 3x − 5

Si  a < 0 (negativo) la parábola es convexa o con puntas hacia abajo, como en f(x) = −3x 2 + 2x + 3


Ecuación polinómica 

f(x)=a.x^2+b.x+c
Se desarrolla utilizando el cuadrado del binomio o aplicando propiedad distributiva.

Ecuación canónica 

f(x)=a.(x-xv)^2+yv
El vértice y el eje de simetría se identifican con facilidad.

Ecuación factorizada

f(x)=a.(X-X1).(X-X2)
Las raíces se identifican de forma inmediata.

Las tres ecuaciones se pueden relacionar de la siguiente forma:

Polinomica a canonica ( se busca el vértice)

Canonica a polinomica ( se desarrolla el cuadrado del binomio o aplicar propiedad distributiva)
Polinomica a factorizada (se buscan las raices)
Factorizada a polinomica (se aplica la propiedad distributiva) 
https://www.youtube.com/watch?v=_ujbUdNZrns 

Sucesiones

Conjuntos numerico: clasificación

Los conjuntos numéricos son construcciones matemáticas que definen diversos tipos de números y que guardan una serie de propiedades estructurales.

El orden de construcción de los conjuntos numéricos (de menor a mayor complejidad) es el siguiente:

Números naturales, entre los cuales se distinguen el numero 1,2,3,4,5 etc.

Los números primos solo pueden ser divisibles por el 1 y por si mismo.

Números compuestos se puede dividir exactamente entre otros números además de 1 y él mismo.

Números pares ejemplo: 2,4,6,8

Números impares ejemplo 1,3,5,7.9

Números enteros: esta conformado por los numeros naturales, sus opuestos (negativos) y el 0.

El número 0, que si bien había sido empleado en diversos lugares, no siempre fue considerado un numero en pie de igualdad con otros números naturales.

Números enteros negativos: todos los numeros menores a 0.

Números enteros positivos (naturales).: mayores al 0.

Los números racionales: es todo número que puede representarse como el cociente de dos enteros, con denominador distinto de cero. 

Números irracionales,  es un número que no se puede escribir en fracción - el decimal sigue para siempre sin repetirse.

Números reales, El conjunto de los números reales pertenece en matemáticas a la recta numérica que comprende a los números racionales y a los números irracionales. Esto quiere decir que incluyen a todos los números positivos y negativos, el símbolo cero, y a los números que no pueden ser expresados mediante fracciones de dos enteros que tengan como denominador a números no nulos (excluye al denominador cero)

EL NUMERO DE ORO

El número áureo (también llamado número de oro, razón extrema y media,1 razón áurea, razón dorada, media áurea, proporción áurea y divina proporción ) es un número irracional, representado por la letra griega φ (phi) (en minúscula) o Φ (Phi) (en mayúscula) en honor al escultor griego Fidias.

Se trata de un número algebraico irracional (su representación decimal no tiene período) que posee muchas propiedades interesantes y que fue descubierto en la antigüedad, no como una expresión aritmética, sino como relación o proporción entre dos segmentos de una recta, es decir, una construcción geométrica. Esta proporción se encuentra tanto en algunas figuras geométricas como en la naturaleza: en las nervaduras de las hojas de algunos árboles, en el grosor de las ramas, en el caparazón de un caracol, en los flósculos de los girasoles, etc.

El numero de oro en la naturaleza: